Окружность на ЕГЭ и ОГЭ — сложно. Все потому, что эта фигура не похожа на остальные: у неё нет углов и сторон, зато есть совсем другие элементы. В этой статье мы подробно поговорим про элементы окружности, углы, отрезки и прямые, которые с ней связаны, а также обсудим длину окружности и площадь круга. Ну и разберем основные задания ЕГЭ и ОГЭ, конечно же!

Все об окружности на ЕГЭ и ОГЭ — разбор заданий и задач
Для начала давайте разберёмся, что же такое окружность. Окружность — это замкнутая линия, состоящая из множества точек, которые равноудалены от центра окружности. Основной элемент окружности — это радиус, он соединяет центр с любой точкой на окружности.
Геометрия на плоскости (планиметрия). Часть II1. Вспоминай формулы по каждой теме2. Решай новые задачи каждый день3. Вдумчиво разбирай решения
(lacktriangleright) Центральный угол – угол, вершина которого лежит в центре окружности. Центральный угол равен дуге, на которую он опирается. (lacktriangleright) Вписанный угол – угол, вершина которого лежит на окружности. Вписанный угол равен половине дуги, на которую он опирается.
(lacktriangleright) Вписанный угол, опирающийся на полуокружность (или на диаметр), равен (90^circ). Задание
15
#3522Уровень задания: Равен ЕГЭНайдите величину острого вписанного угла, опирающегося на хорду, равную радиусу окружности. Ответ дайте в градусах.
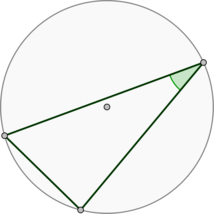
Обозначим хорду за (AB). Рассмотрим ( riangle AOB), где (O) – центр окружности.
Так как (AB) равна радиусу окружности, то ( riangle AOB) – равносторонний. Следовательно, (angle
AOB=60^circ). Заметим, что (angle AOB) и (angle ACB) – центральный и вписанный углы, опирающиеся на одну и ту же дугу, следовательно, (angle ACB=0,5angle AOB=30^circ). Задание
16
#633Уровень задания: Равен ЕГЭХорда (CD) перпендикулярна диаметру (AB). Найдите разность градусных мер дуг (AC) и (AD) (тех, которые меньше полуокружности). Ответ дайте в градусах. Построим отрезки (CA), (AD) и (CB), точку пересечения (CD) и (AB) обозначим (E).
Задание
17
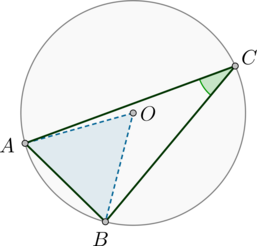
#3104Уровень задания: Равен ЕГЭСторона (AB) тупоугольного треугольника (ABC) равна радиусу описанной около него окружности. Найдите тупой угол (C). Ответ дайте в градусах.
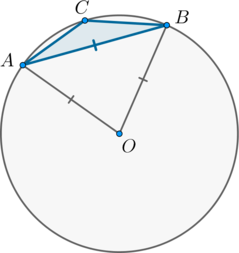
Задание
18
#631Уровень задания: Сложнее ЕГЭ
Задание
19
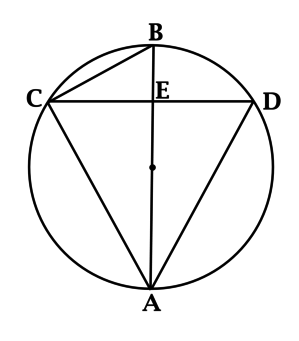
#2160Уровень задания: Сложнее ЕГЭНа рисунке (O) – центр окружности, (AO=OB=BC=CA). Найдите угол (ADC). Ответ дайте в градусах.
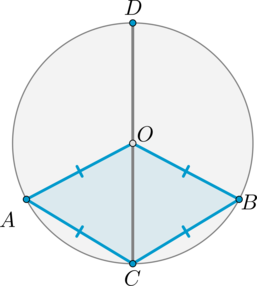
Четырехугольник, все стороны которого равны, является ромбом. Следовательно, (AOBC) – ромб. Значит, диагонали делят его углы пополам. Следовательно, (angle AOC=angle BOC=angle ACO=angle
BCO=x).
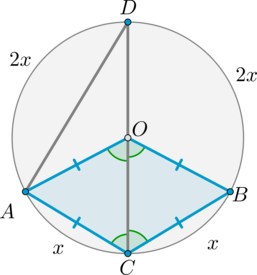
вся окружность равна (360^circ), то (x+x+2x+2x=360^circ quad
Rightarrow quad x=60^circ). Задание
20
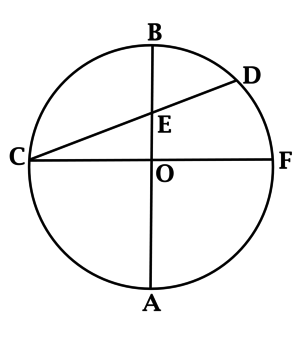
#2158Уровень задания: Сложнее ЕГЭСекущая (AB) пересекает окружность и диаметр (CD) так, как показано на рисунке.
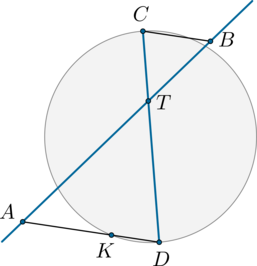
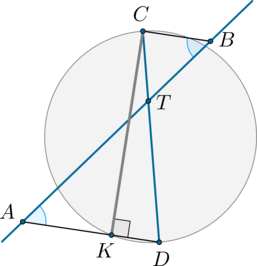
(BCparallel AD), то (angle CBT=angle DAT=30^circ). (angle
DCK), как вписанный и опирающийся на дугу (KD), равен ее половине, то есть (20^circ). (angle CKD) опирается на диаметр (CD), следовательно, равен половине от половины окружности, то есть (90^circ). Значит, (angle CDK=180^circ -90^circ
-20^circ=70^circ). (angle BTD) — внешний угол для треугольника (ATD), следовательно, он равен сумме двух углов треугольника, не смежных с ним: (angle
BTD=angle TDA+angle TAD=30^circ+70^circ=100^circ). Задание
21
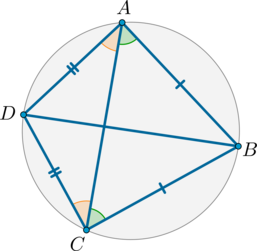
#2157Уровень задания: Сложнее ЕГЭНа окружности в следующем порядке отмечены четыре точки: (A), (B), (C) и (D), причем (AB=BC, CD=DA). Найдите угол (BAD). Ответ дайте в градусах.

Центральные и вписанные углы окружности(lacktriangleright) Центральный угол – угол, вершина которого лежит в центре окружности. Центральный угол равен дуге, на которую он опирается. (lacktriangleright) Вписанный угол – угол, вершина которого лежит на окружности. Вписанный угол равен половине дуги, на которую он опирается.
(lacktriangleright) Вписанный угол, опирающийся на полуокружность (или на диаметр), равен (90^circ). Задание
1
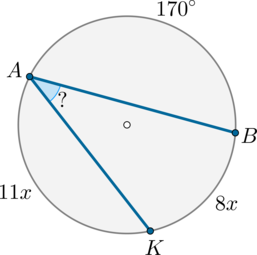
#2156Уровень задания: Равен ЕГЭТочки (A) и (B) делят окружность на две дуги, одна из которых равна (170^circ), а другая точкой (K) делится в отношении (11:8), считая от точки (A). Найдите (angle BAK). Ответ дайте в градусах.
Задание
2
#2159Уровень задания: Равен ЕГЭХорды (KN) и (LM) взаимно перпендикулярны. Найдите угол (NLM), если угол (KML) равен (35^circ). Ответ дайте в градусах.
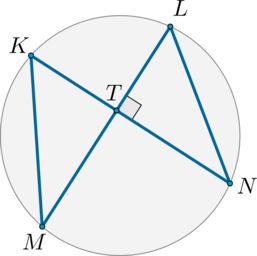
Вписанные углы (KML) и (KNL) опираются на одну и ту же дугу, следовательно, они равны, значит, (angle KNL=35^circ). Тогда (angle NLM=180^circ-90^circ-35^circ=55^circ). Задание
3
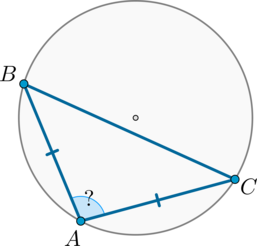
#2155Уровень задания: Равен ЕГЭТочки (A) и (C) разбивают окружность на две дуги, одна из которых равна (280^circ) и на которой отмечена точка (B). Найдите угол (BAC), если (AB=AC). Ответ дайте в градусах.
Задание
4
#630Уровень задания: Равен ЕГЭТочки (A), (B), (C) и (D) лежат на окружности с центром в точке (O) (так, что (ABCD) – четырёхугольник). Длина дуги (AD) (которая меньше полуокружности) составляет (0,8) длины дуги (AB) (которая меньше полуокружности). Найдите, во сколько раз (angle AOB) больше, чем (angle DCA).
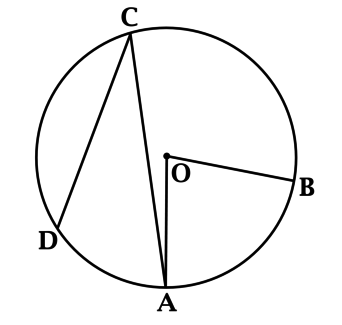
Градусные меры дуг окружности относятся как их длины, тогда градусная мера дуги (AB) в (1: 0,8 = 1,25) раз больше, чем градусная мера дуги (AD). Градусной мерой дуги называется градусная мера центрального угла, который на неё опирается. Задание
5
#632Уровень задания: Равен ЕГЭ
Задание
6
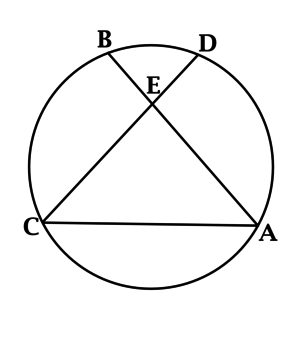
#3531Уровень задания: Равен ЕГЭЧетырехугольник (ABCD) вписан в окружность. Угол (ABD) равен (75^circ), угол (CAD) равен (35^circ). Найдите угол (ABC). Ответ дайте в градусах.
Задание
7
#3523Уровень задания: Равен ЕГЭЧему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

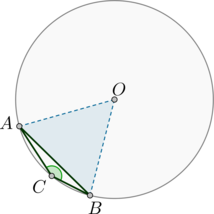
Отрезки и прямые в окружности на ЕГЭ и ОГЭ
Теперь рассмотрим отрезки и прямые в окружности. Приготовьтесь, их будет много!
Есть хорда — это отрезок, который соединяет 2 любые точки на окружности. Если хорда пройдёт через центр окружности, то она превратится в диаметр. Кстати, если внимательно посмотреть, то можно увидеть, что диаметр — это 2 радиуса!
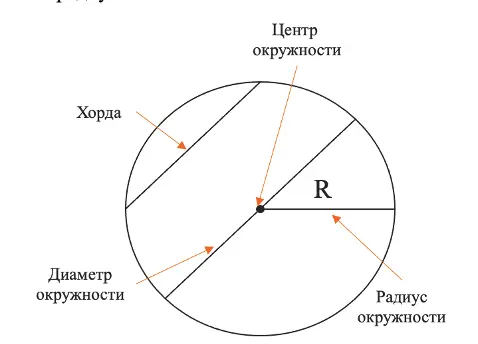
Хорда, диаметр, радиус и центр окружности на схеме
Теперь продлим хорду в обе стороны за пределы окружности, получим прямую, которая переСЕКает нашу окружность, отсюда и её название — секущая. Можно заметить, что секущая имеет 2 общих точки пересечения с окружностью. А ещё мы можем провести прямую так, чтобы она имела с окружностью только 1 точку пересечения, то есть касалась её, такая прямая будет называться касательная.
Подробнее со свойствами касательной и секущей можно ознакомиться на рисунке:
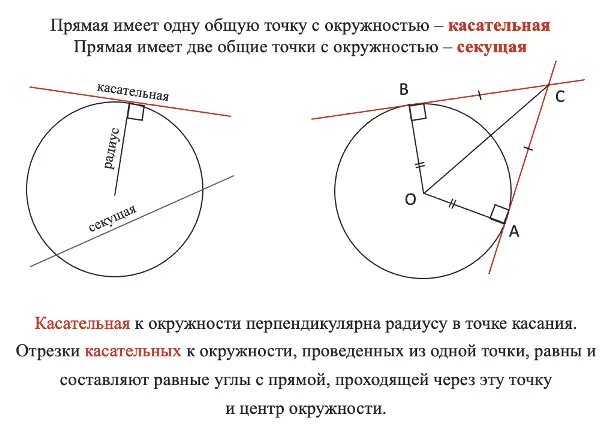
Свойства касательной и секущей в окружности на схеме
Рассмотрим на примерах заданий про окружность в ЕГЭ и ОГЭ:
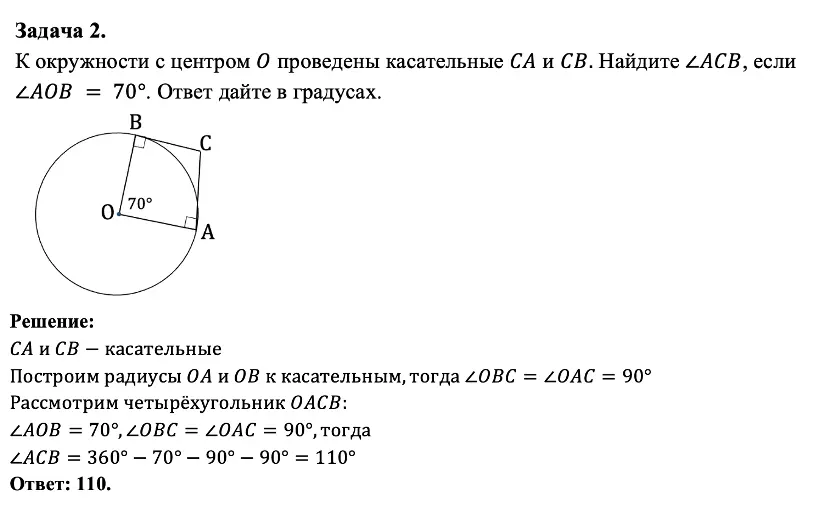
Первый пример задания на касательную в окружности на ЕГЭ и ОГЭ
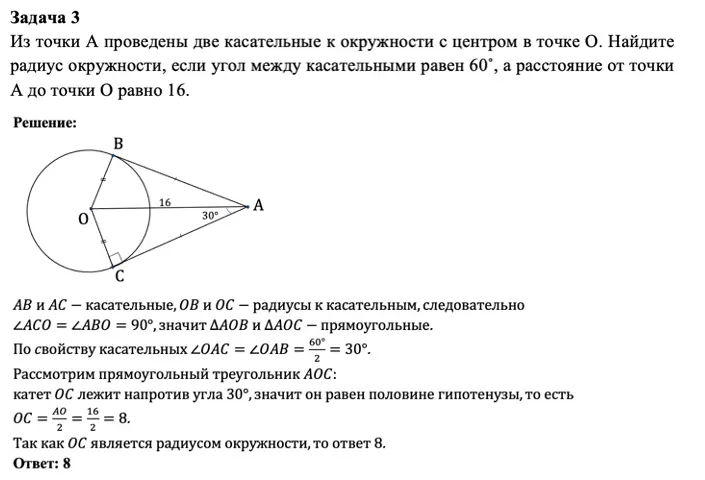
Второй пример задания на касательную в окружности на ЕГЭ и ОГЭ
4 теоремы про окружность в ЕГЭ и ОГЭ
Теперь я предлагаю ознакомиться с теоремами, которые появляются в комбинациях различных прямых и отрезков в окружности.
Теория и задания из ЕГЭ и ОГЭ
Первая теорема про хорду и касательную звучит так:
Угол между касательной и хордой равен половине дуге, которую стягивает хорда.
Подробнее с выведением вы можете ознакомиться на рисунке:
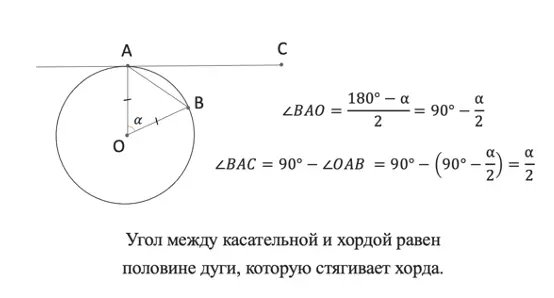
Вот так выводится теорема про хорду и касательную
Однако хочу обратить ваше внимание, что если вы просто запомните формулировку, то многие задачи на окружность в ЕГЭ и ОГЭ покажутся вам супер-простыми и будут решаться в 1 действие. Давайте в этом убедимся:
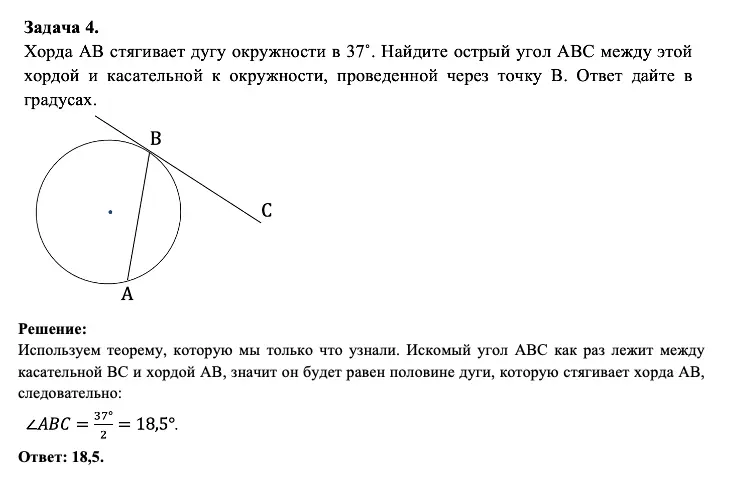
Пример решения задачи на окружность в ЕГЭ и ОГЭ с использованием теоремы про хорду и касательную
Вот так просто и быстро в 1 действие мы справились с задачей. Правда здорово?!
А теперь давайте посмотрим на одну из моих самых любимых теорем. А любимая она, потому что без неё некоторые задачи кажутся практически нерешаемыми, а с ней их можно решить быстро и просто! Звучит она так:
Квадрат касательной равен произведению секущей на её внешнюю часть. Я советую запоминать именно словесную формулировку, так как чертежи и буквы на них могут быть разными, и есть риск всё перепутать.
Наглядно познакомиться с теоремой можно на рисунке ниже:
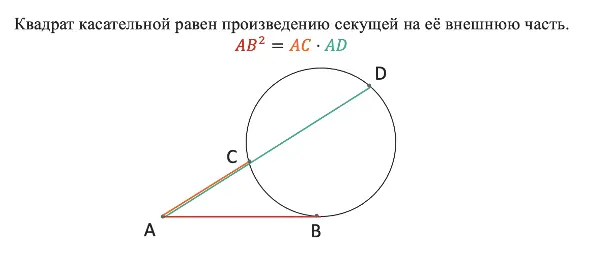
Теорема: квадрат касательной равен произведению секущей на её внешнюю часть
И конечно же давайте отработаем на практике!

Если бы мы не знали ту теорему, которую только что прошли, то было бы много версий, как можно решить задачу. Кто-то начал бы строить радиус к касательной и рассматривать треугольники, а кто-то просто не стал бы решать, однако у нас есть формула: давайте её используем!
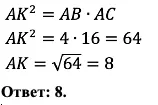
Вот так просто решается это задание!
Если вы ещё не устали от теорем, то давайте познакомимся с ещё одной, которая связывает хорду с диаметром (радиусом).
Эта теорема интересна тем, что работает в обе стороны:
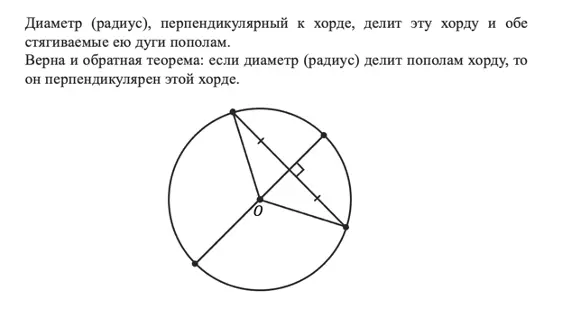
Вот так хорду можно связать с диаметром (радиусом)
Конечно же я не могу оставить вас без тренировки, поэтому посмотрим на следующую задачу:

Задание на нашу теорему и его решение
Пересекающиеся хорды
Последнее, с чем я вас познакомлю в контексте прямых и отрезков в окружности будет свойство пересекающихся хорд:
Произведения отрезков пересекающихся хорд равны.
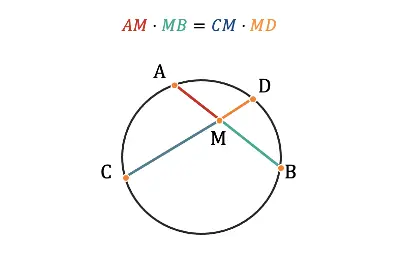
Свойство пересекающихся хорд на рисунке
Для наглядности отрезки выделены разными цветами, так вам будет проще запомнить свойство.
А теперь отработаем его на практике:
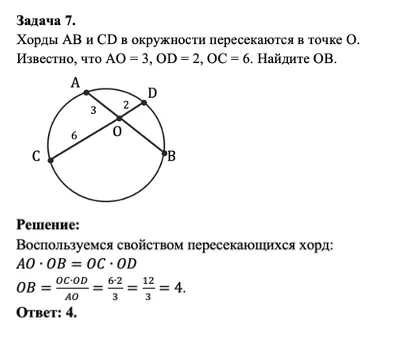
Задание на свойство пересекающихся хорд и его решение
Что нужно иметь в виду для ЕГЭ и ОГЭ
На самом деле это всё, что я хотела вам рассказать в данной статье. Давайте ещё раз повторим, что вы узнали.
- Сначала мы познакомились с понятием окружность, потом посмотрели, какие бывают углы в окружности.
- Затем увидели множество отрезков и прямых в окружности, записали их свойства, а также несколько теорем с ними.
- В завершение мы поговорили про длину окружности, площадь круга, а также поиск площади и длины дуги сектора.
Самое ценное, что всю теорию мы закрепили на реальных заданиях из ОГЭ и ЕГЭ. Конечно, это далеко не всё, что вам может встретиться. Если вы хотите хорошо разбираться в окружности и в других темах, которые встречаются на экзаменах, записывайтесь на наши курсы подготовки к ОГЭ и ЕГЭ. На них мы подробно изучаем всю теорию, решаем много заданий, запоминаем удобные лайфхаки и решаем пробные экзамены, чтобы не стрессовать на реальном. Присоединяйтесь!
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

ㄥAOB = ◡ AB

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Хорда — отрезок, соединяющий две точки на окружности.


AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

ㄥBAC + ㄥBDC = 180°
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° −
AC −
CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½. ㄥACB = ½
AB = 40°
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол. На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½
AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от
CB = 72° / 2 = 36°
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности. Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Длина окружности и площадь круга
Вот мы и подошли с вами к самому интересному, формулам длины окружности и площади круга, давайте их запишем:

Формулы длины окружности и площади круга
Эти формулы очень походы, в них есть двойка, число Pi и радиус, однако можно заметить, что у формулы длины окружности двойка слева, а у площади круга справа в степени.
Так как же их не путать? Очень просто: запомните, что вторая степень (или квадрат) должна быть у площади, значит двойка слева будет у длины.
Давайте это закрепим:

Задание на длину окружности и площадь круга в ЕГЭ и ОГЭ
Вот так просто и быстро мы закрепили сразу обе формулы.
Как находить площадь и длину дуги сектора круга
А теперь перейдём к самому интересному — нахождению площади и длины дуги сектора круга. Многие ученики думаю, что это сложно, но на самом деле это не так. Я предлагаю записать 2 коротких алгоритма, с помощью которых вы сможете легко найти площадь или длину дуги сектора.

2 алгоритма для поиска площади и длины дуги сектора
И конечно же давайте закрепим эти алгоритмы на практике:

Задача на поиск площади сектора круга в ЕГЭ и ОГЭ
Теперь вы умеете решать задания на поиск площади сектора. Согласитесь, что с алгоритмом всё намного понятнее и проще?
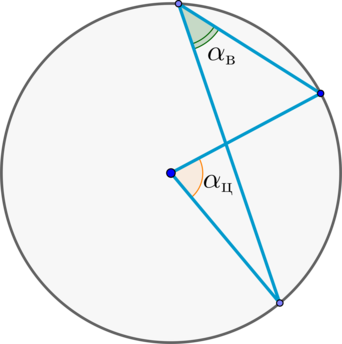
Углы у окружности на ЕГЭ и ОГЭ
У окружности есть 2 вида углов:
- вписанные (их вершина лежит на окружности);
- центральные (тут всё понятно из названия, у них вершина в центре окружности).
Расположение и свойства углов в окружности можно увидеть на схеме ниже:
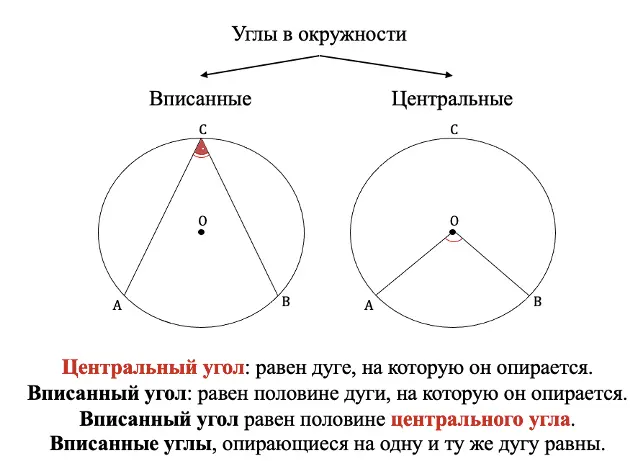
Теория: углы в окружности на ЕГЭ и ОГЭ
Давайте отработаем это на практике:

Задание на углы окружности в ЕГЭ и ОГЭ
Решение
Можно заметить, что угол АСВ — вписанный и опирается на дугу АВ, соответственно, центральный угол АОD, опирающийся на ту же дугу будет в 2 раза больше, то есть 70 градусов. Теперь рассмотрим развёрнутый угол ВОD, он состоит из углов АОВ и АОD. Градусная мера развёрнутого угла 180 градусов, следовательно искомый угол АОD будет равен 180 – 70 = 110 градусов.